É impensável imaginar o mundo tal como o sentimos sem a
MATEMÁTICA. Se tal fosse possível, o nosso posicionamento
cultural, científico e tecnológico seria muito diferente e
certamente
pior. O obscurantismo e a irracionalidade seriam predominantes, a
ciência e a tecnologia muito limitadas e a nossa capacidade de
atacar
os problemas seria essencialmente emocional, assente em crenças
e sem lógica. Parece-me lícito afirmar que, ao longo dos séculos, o
desenvolvimento da MATEMÁTICA tem contribuído para um
MUNDO MELHOR, ou seja, um mundo culturalmente,
cientificamente e tecnologicamente mais desenvolvido.
Galileu Galilei (1564-1642) referiu que apenas se pode entender a
Natureza quando se aprende a sua linguagem e os seus sinais; mas
essa linguagem é MATEMÁTICA e esses sinais são figuras
matemáticas. Por sua vez, o filósofo Immanuel Kant (1724-1804)
afirmou que em qualquer das ciências naturais a substância
científica genuína é proporcional à matemática que apresenta. Sem
MATEMÁTICA a Astronomia e a Física dos nossos dias seriam
impossíveis; os ramos teóricos destas ciências dissolvem-se
virtualmente em MATEMÁTICA.
De acordo com o matemático David Hilbert (1862-1943), a
MATEMÁTICA é a ferramenta intermediária entre a teoria e a prática,
entre pensamento e observação.
As origens da MATEMATICA perdem-se no tempo e nos primórdios
da humanidade. Os vestígios de formas e números são pré-históricos.
As
aplicações da aritmética no controlo de sistemas de
irrigação, entre outros, estão registadas como práticas de alguns
povos e culturas que, entre 3000 e 525 a.C., se fixaram ao longo dos
grandes rios da África e da Ásia (Nilo, Tigre e Eufrates). Os
babilônios, que viveram entre 2000 a.C. e 1600 a.C., dividiram o
círculo em 360 partes e constataram que uma circunferência tinha o
triplo do seu diâmetro, o que correspondia a atribuir a π o valor 3.
Neste período, a MATEMÁTICA já não se reduzia à aritmética, incluía
também expressões algébricas que formulavam problemas cujas
soluções procuravam obter. A MATEMÁTICA, no sentido em que
atualmente a conhecemos, onde a demonstração desempenha um
papel fundamental, teve o seu início no sexto século a.C., com a
geometria de Tales de Mileto, um dos sete sábios da Grécia Antiga
(segundo o filósofo e matemático Platão, fundador da Academia de
Atenas, estes sete sábios são Tales de Mileto, Pítaco, Bias de
Priene, Sólon, Cleóbulo de Lindos, Míson de Queneia e Quilão de
Esparta). Os Elementos de Euclides que consistem num tratado
matemático escrito em 13 livros por volta de 300 a.C., dominaram os
primeiros séculos da MATEMÁTICA grega. Este tratado introduz a
primeira abordagem axiomática de uma teoria, a geometria
euclidiana, e de certo modo obscureceu tudo o que antes dele se
produziu. David Hilbert dizia: pode medir-se a importância de um
trabalho científico pelo número de publicações que ele tornou
supérfluas.
Apesar dos inúmeros avanços da MATEMÁTICA, conseguidos até
ao final do século XVII, é nessa altura que ela atinge o seu patamar
superior com o aparecimento do Cálculo Infinitesimal introduzido de
forma independente pelos matemáticos Isac Newton (1642-1727) de
nacionalidade britânica e Gottfried Wilhelm Leibniz (1646-1716) de
nacionalidade alemã, dando início à MATEMÁTICA dos tempos
modernos que desde então tem conhecido um desenvolvimento
esmagador com implicações científicas notáveis.
Durante os últimos séculos, a MATEMÁTICA subdividiu-se em várias
subáreas que se desenvolveram autonomamente com elevado grau
de especialização, entre as quais podemos destacar a Álgebra,
Análise, Combinatória, Geometria, Lógica e Teoria dos Números,
entre muitas outras. Estas subáreas deram à MATEMÁTICA uma
estrutura complexa com fronteiras difíceis de traçar e relações por
vezes muito surpreendentes. Consta que o matemático e astrónomo
alemão Carl Friedrich Gauss (1777-1855) foi a última pessoa a
conhecer toda a MATEMÁTICA do seu tempo.
Apesar do matemáticfo britânico Godfrey Hardy (1877-1947) ter
escrito: nenhuma das minhas descobertas fez, ou poderá fazer,
direta ou indiretamente, para o bem ou para o mal, a menor diferença
para o mundo, numa carta que em 1908 enviou ao American Journal
of Science, com uma abordagem algébrica muito simples,
demonstrou que havia um erro num artigo sobre a teoria genética de
Mendel (segundo a qual os seres vivos herdam o gene dominante)
versus a teoria da seleção natural de Darwin (de acordo com a qual
se uma caraterística é benéfica para a sobrevivência e procriação de
um ser vivo, então ela acaba por prevalecer), introduzindo um
princípio de equilíbrio hereditário. No mesmo ano, o médico alemão
Wilhelm Weinberg chegou a um princípio semelhante que acabou por
se designar princípio de Hardy-Weinberg.
Com efeito, a MATEMÁTICA tem-se revelado muito poderosa no
estudo e compreensão da natureza. Por exemplo, Fibonacci, também
conhecido por Leonardo de Pisa, numa publicação de 1202 com o
título Liber abaci, introduziu a sequência (F0,
F1, …,
Fj-2,
Fj-1,
Fj, … ),
conhecida por sequência de Fibonacci, onde F0=0 e
F1=1 e os
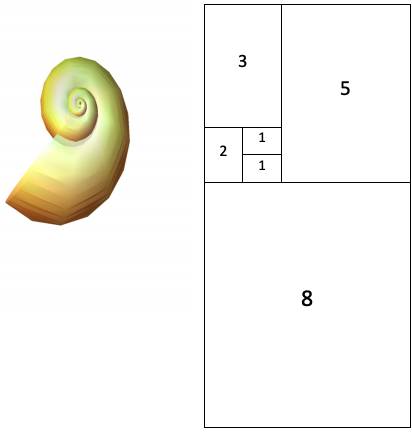
restantes termos são a soma dos dois anteriores. Transformando
estes números em lados de quadrados geométricos, define-se uma
espiral (conhecida por espiral de Fibonacci) que determina um
padrão geométrico existente em vários animais e plantas, como são
o caso dos abacaxis, girassóis, conchas, etc.
O físico alemão Albert Einstein (1879-1955) escreveu: como é
possível que a matemática, um fruto do pensamento, se encaixe tão
bem à realidade física? Ou seja, a MATEMÁTICA parece não ser
apenas a linguagem da Natureza, mais do que isso, tem-se revelado
como a linguagem do Universo. No entanto, através dela, ainda não
foi possível explicar as quatro forças que unificam o cosmus
(gravidade, eletromagnetismo e as forças nucleares fortes e fracas,
todas tão distintas), bem como a surpreendente coleção das
partículas subatómicas.
Não se sabe se a MATEMÁTICA é uma criação humana ou é apenas
descoberta (ou seja, sempre existiu e nós apenas a vamos
descobrindo). Se for uma criação humana, a probabilidade de uma
civilização extraterrestre criar a mesma MATEMÁTICA é
extremamente diminuta e por isso muito dificilmente poderia ter uma
perceção do Universo idêntica à nossa. Como consequência, seria
praticamente impossível detetá-la ou serem eles a detetarem-nos a
nós.
Termino estas notas com uma referência ao matemático português
Francisco Gomes Teixeira (1851-1933) que se formou na
Universidade de Coimbra, onde também se doutorou em 1875 e em
1880 assumiu as funções de Professor Catedrático. Quatro anos
mais tarde, pediu a transferência para a Academia Politécnica do
Porto, percursora das atuais Faculdades de Ciências e de
Engenharia da Universidade do Porto, da qual em 1911 veio a ser o
primeiro Reitor. Segundo Gomes Teixeira, um trabalho matemático
é, para quem o sabe ler, o mesmo que um trecho musical para quem
o sabe ouvir, um quadro para quem o sabe ver, uma ode para quem
a sabe sentir. Trata-se de uma visão alternativamente
inspiradora e
igualmente motivadora para se continuar a estudar e investigar
(criar
ou descobrir) MATEMATICA e para se poder afirmar que a
MATEMÁTICA indubitavelmente tem contribuído e certamente
continuará a contribuir para um MUNDO MELHOR.
Bibliografia
Howard Eves, Introdução à História da Matemática, 2ª Edição,
Editora da
Universidade Federal de Campinas, Campinas 1997.
Ioan James. Remarkable Mathematicians – from Euler to von Neuman,
Cambridge University Press, Cambridge UK 2004 (reprint).
Michio Kaku, Hiperespaço – uma odisseia científica através
de
universos
paralelos, de dobras temporais e da 10ª dimensão, Editorial
Bizâncio, Lisboa
2016.












.jpg)